Fast Block Dissemination with Immediate Guarantees

You can come to consensus over a mere fingerprint of the block—a hash for example— but doing anything interesting with that fingerprint, like processing transactions or updating state, requires disseminating (a lot of) data.

We’ve invested some effort in this part of the Commonware Library recently, and I’d like to share some fruits of that effort in this post. As an outline, we’ll cover:

• data dissemination, naively,
• how to increase efficiency with coding,
• and, finally, how to get quicker guarantees about the data with ZODA.

ZODA is particularly exciting, because it achieves the guarantees of something like Reed-Solomon + KZG, without requiring a trusted setup, and while being more performant, and having less data transmission overhead.

In a future post we will cover lower-level details of our implementation, like the field we use for Reed-Solomon coding, and the optimizations needed for fast fourier transforms, but this one will stick to an overview.

Naive Dissemination

We assume a leader has some data, \(D\) bytes worth, to be disseminated. They want \(m\) followers to receive it. The simplest approach is to have the leader send the data to every follower. The leader’s transmission cost is \(m \cdot D\) bytes, and the followers’ cost is \(0\) bytes, since they send nothing.

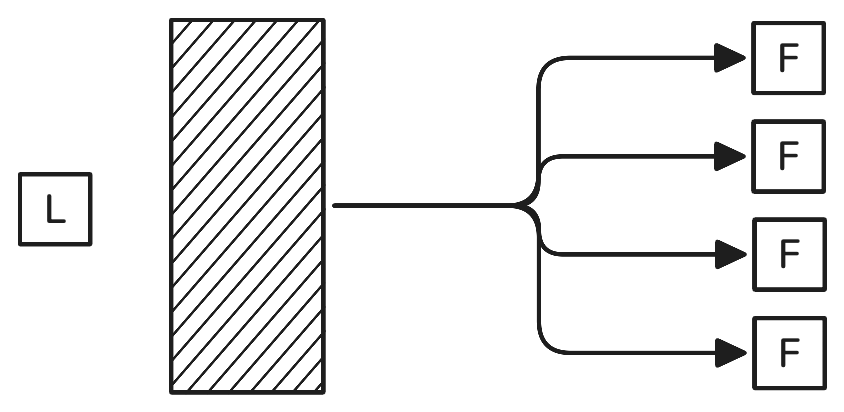
Networked protocols are often bottlenecked by sending data, since moving bits around the planet, a country, or a building is hopelessly slow compared to moving it within an integrated circuit.

Some back-of-the-napkin math: if our leader has a 1 Gb / s link, and needs to send a 1 MB block to 50 followers, we would expect this to take at least 400 ms, assuming no overhead at all in transmitting. The commonware-estimator can be used to test out this example.

This protocol is bottlenecked more so, with all of its communication going through the single leader node. While the leader sends the entire data \(m\) times, the followers sit idle, wasting their resources. We can do better.

Towards Coding

We want the followers to participate in sending the data as well. Imagine, after our naive protocol, that a follower crashes, losing their data. This is no big problem: the data is present among the other followers, and our lost node can communicate with them to recover it. In fact, every other node has all of the data, so you have more information than required on the network. If one node had one half of the data, and some other node the other half, you would still be able to recover it, by combining their halves.

We could extend the logic further still: each of the \(m\) participants could hold \(\frac{1}{m}\) of the data. All together, the participants hold it all, distributed as thinly as possible. (They do still need to communicate to recover the data, of course, but it is recoverable).

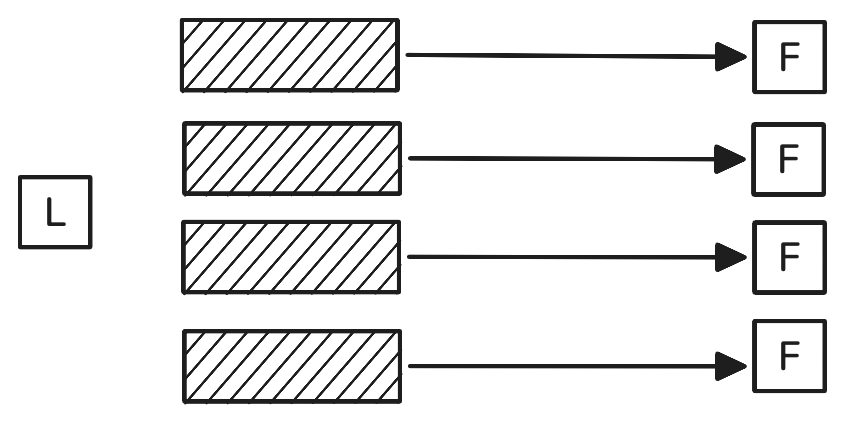
In this case, the leader’s transmission cost is now just \(m \cdot \frac{D}{m} = D\), quite the improvement. If the participants want to recover the whole data, each of them will need to send their shard to the others, at a cost of \((m - 1) \cdot \frac{D}{m}\) bytes. The total amount of data sent by the leader, and then the followers, is \(D + m \cdot \frac{(m - 1) D}{m} = m \cdot D\). Compared to the naive approach, the total amount of data sent is the same. However, it is sent much more efficiently, spreading the load evenly across all the links in the network. Each node sending \(\frac{(m - 1)}{m} \cdot D\) bytes worth of data to others can operate in parallel, whereas in the original case, the leader must send \(m \cdot D\) bytes sequentially.

Dealing with Loss

One flaw in our scheme, so far, is that the data is spread so thinly, that even one node missing out results in it being lost completely. This might happen by accident—a node crashing is not impossible, after all— but we also want to tolerate malicious nodes. One follower being able to block transmission is not acceptable.

From here, we reach to using a coding scheme. This scheme takes in a message of \(n\) symbols—we shall revisit the term, but think of it like a small, consistently sized piece of data, e.g. a byte—and produces \(m \geq n\) symbols. A useful coding scheme has the property that given any \(n\) of these \(m\) symbols, we can recover the original message.

As an example, a Reed-Solomon code consists of treating the data as a list of \(n\) field elements (essentially, elements of some set where addition, multiplication, and division make sense) which define the polynomial:

\[ d(X) \coloneqq a_0 + a_1 X + \cdots + a_{n - 1} X^{n - 1} \]

We can then consider the evaluation of this polynomial at \(m\) distinct points:

\[ d(\omega_0), d(\omega_1), \ldots, d(\omega_{m - 1}) \]

as forming our encoded message. With some algebra, any \(n\) of these evaluations can be interpolated back into the original polynomial \(d(X)\), whose coefficients spell out our message.

We have an implementation of this scheme here.

These details are not essential: what matters is that we take \(n\) symbols, encode them into \(m\), such that any \(n\) of the encoded symbols are good enough to recover the originals.

Dissemination with Coding

This naturally suggests a scheme in which followers receive encoded symbols, allowing recovery with partial information. To flesh this out further, we want to accommodate data which may not consist of precisely \(n\) symbols. Instead, we assume a matrix of \(n \times c\) symbols (which may be padded). This matrix can be encoded columnwise, producing a result of size \(m \times c\). Each shard can be a row of this matrix. Given \(n\) shards, the original matrix can be recovered, proceeding columnwise once more.

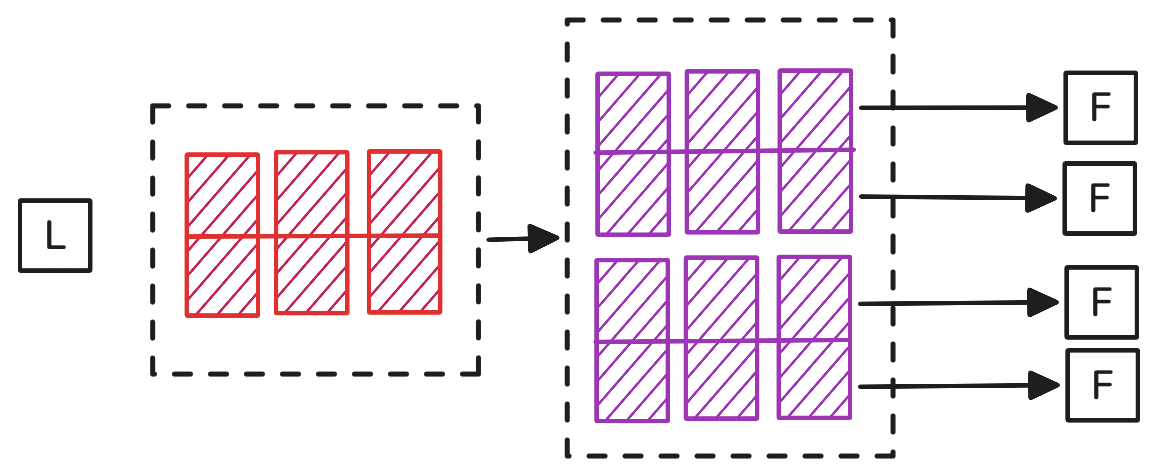
The cost of this scheme is now: - \(m \cdot \frac{D}{n}\) for the leader, - \((m - 1) \cdot \frac{D}{n}\) for each follower, - \(\frac{m^2}{n} \cdot D\) in total.

As the redundancy decreases, with \(m \to n\), we get the same cost as before. We want some redundancy though, with \(m \gg n\), so the total cost will be higher than before. Nevertheless, it is distributed far more fairly than the naive case, so we should expect data to be disseminated more quickly all else being equal.

Integrity

We’ve described coding schemes as being able to tolerate erasure: missing pieces of data. This fits naturally in the model of crash faults: if a node crashes, their piece is lost, but we can tolerate this. What do we do in the case of malicious faults, where data is intentionally changed, rather than merely omitted?

Some coding schemes can tolerate random errors. For example, bit flips, or adding a random field element. Unfortunately, this comes at the cost of at least doubling the amount of redundancy in order to correct the same number of errors. There’s also a significant jump in algorithmic complexity, mathematically, and cognitively, to the point where implementations often don’t contain procedures for decoding with errors at all.

To avoid the need to correct errors, we can use a trick: instead of decoding with bad shards, we could detect that they’ve been corrupted, and treat them as missing instead.

If the followers received a hash of each shard, then they could tell whether some data is actually the shard it claims to be, by hashing it. This comes at a penalty of transmitting \(m \cdot 2^\lambda\) bits of data (guaranteeing no collisions up to a probability of \(2^-\lambda\) requires \(2 \lambda\) bit hashes). We can improve this a bit by having the leader use a vector commitment over the \(m\) hashes. Each shard would then come with an opening, demonstrating that the \(i\)th hash in the vector is that of the shard. A binary Merkle Tree is an example of such a scheme (but others might work better, e.g. playing with arity, or using a Polynomial Commitment Scheme).

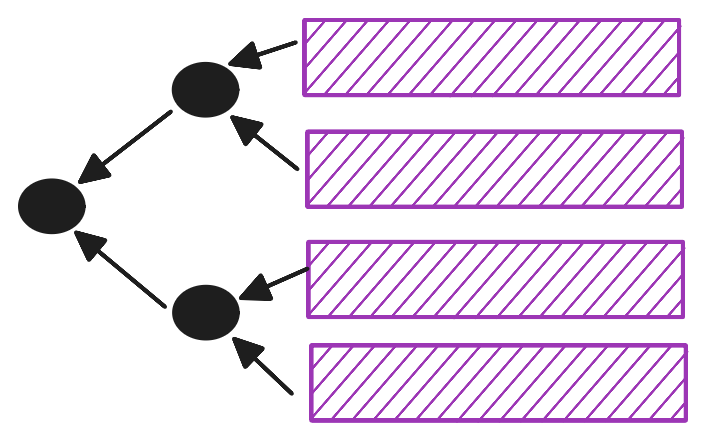
As a side-effect, our scheme now produces a fingerprint, attesting uniquely to the encoded data. This could be used for consensus, like the hash of the data itself often is.

Bad Leaders

So far, our leader encodes the data into shards, distributes them, and given a large enough subset of them, we can recover the data. We also know that a malicious follower cannot tamper with the data, because they must prove that their shard is what the leader committed to.

But, what if the leader is malicious? What if instead of encoding data into shards, they simply made the shards up themselves?

In that case, honest followers might successfully reconstruct something, but each of them sees a different result, based on the particular shards they chose to use. It’s also easy to get different honest followers to pick different shards, by selectively withholding them. Proceeding with different data is very bad, so we want to avoid this.

Something we can do is to check that re-encoding the data produces what the leader claimed. If encoding is: - deterministic, producing, always, the same result, - injective, with different data producing different results, then this works out. A malicious leader shares one commitment, and there can be at most one original piece of data that commits to that value.

One drawback is that now we can only know that the data exists after we’ve reconstructed it. If we’re tying this process to consensus, it would be nice to avoid coming to agreement on a piece of data which will turn out to never have existed, producing an empty block. There’s also, more plainly, a cost to re-encoding, which it might be nice to avoid.

ZODA

At a high level, ZODA allows us to avoid this issue. We can be convinced that our shard comes from a valid encoding of some unique piece of data, as soon as we receive our shard.

(For ZODA afficionados, what we describe subsequently is the application of the “Hadamard” variant from section D of the paper).

This involves sending, along with the shard, some additional data, of use not in recovering it, but in providing assurance that our shard results from an encoding of it.

Some Details and Intuition

The inner workings of the protocol are not necessary to understand its utility nor application, but are simple enough to be understood at a high level of operation.

We continue in modelling our data, \(X\), as a matrix of dimension \(n \times c\), with elements in some field \(F\). We can encode it, using a matrix \(G\) of dimension \(m \times n\), producing \(Y \coloneqq G X\), of dimension \(m \times c\). The rows of \(Y\) are committed to, and this commitment can serve as a source of randomness in what follows, according to the Fiat-Shamir paradigm.

Whereas in the plain coding scheme, we received one particular row of \(Y\), here we receive \(S\) rows, sampled at random. (We may modify \(m\) and \(n\) to accomodate this fact). We also receive proofs of inclusion for each row.

In order to convince us that our rows \(Y_S\) came from \(G X\), a random matrix \(H\) of dimension \(c \times S'\) is sampled from a (potentially) larger field \(F' \supseteq F\). Then, we are given \(Z \coloneqq X H\), of dimension \(n \times S'\).

Because encoding is linear, we can check that:

\[ Y_S H \overset{?}{=} (G Z)_S \]

which should hold for an honest encoder, since:

\[ G (X H) = (G X) H \]

for any matrices \(G\), \(X\), \(H\).

Some Intuition

You can show, as the paper does, that given enough samples \(S\), \(S'\), and a large enough \(F'\), any desirable level of security can be achieved. We can, however, reason intuitively about why this might work.

For a given row \(Y_i\), checking:

\[ (Y_i H)_j \overset{?}{=} (G Z)_{i j} \]

is the same as checking that a random linear combination of (alleged) encoded symbols is equal to \(G x\), for some symbol \(x\). In other words, that this combination is an encoded symbol. This is true if \(Y_i\) is correct, and likely to be false if not. By sampling \(S'\) check columns, we perform this check many times, with different randomness, making it more likely to be false for a fake encoding. Furthermore, by sampling \(S\) rows at random, rather than having a row assigned to use by the leader, we make it very difficult to find some clever data which will slip through our checks, since the cheater will not know where they need to fake the outcome.

Completing the Protocol

To complete the sketch of the protocol let’s look at how we handle the shards, collectively. Rather than have each follower sample \(S\) rows at random, we instead shuffle the rows, and partition it into chunks of size \(S\). This guarantees no overlap between shards, while still giving us the randomness to convince us of a valid encoding. When receiving shards, we check inclusion, and that:

\[ Y_S H \overset{?}{=} (G Z)_S \]

as for our own shard.

Comparisons with KZG

Another approach to verifiable dissemination is to lean into Polynomial Commitment Schemes. This is, in essence, how Danksharding works.

In the case of Reed-Solomon coding, each shard is the evaluation of some polynomial \(d(X)\) at a given point. The problem of checking that our shard is an evaluation of a claimed polynomial is exactly that solved by a PCS. Such a scheme produces a succinct commitment to \(d(X)\), such that we can also prove that some data is the result of evaluating \(d(X)\) at a given point, which is what we need.

The ZODA paper has some comparison numbers with such a scheme, using KZG commitments, but they should be taken with a fairly large grain of salt, since they analyze things from a data availability stand point, where you have a large number of samplers (around 1000), with a rate (i.e. \(n / m\)) of \(1/2\). For the use-case of data dissemination, you’d likely have fewer nodes (around 100, or however many validators you have), with a higher rate (something like \(2/3\), allowing you to recover if byzantine validators omit their shards). Nonetheless, you can compare the claimed performance for different data sizes. For each scheme, the original block size, the size of each shard, and the total size of all shards is reported. The inefficiency—how much data is needed compared to just sending all of the data naively–is also reported.

Block size	ZODA Node	ZODA Network	Zoda Inef.	2D KZG Row/Col Node	2D KZG Row/Col Net.	2D KZG Row/Col Inef.
32MiB	1.04 MiB	72 MiB	2.3x	12 MiB	271 MiB	8.5
256MiB	2.84 MiB	560 MiB	2.2x	35 MiB	2.0 GiB	8.2
1GiB	7.68 MiB	2.1 GiB	2.1x	70 MiB	8.1 GiB	8.2
32GiB	43.2 MiB	66 GiB	2.1x	394 MiB	258 GiB	8.1
1TiB	244 MiB	2.1 TiB	2.1x	2.2 GiB	8.1 TiB	8.1

In any case, we can see a claimed improvement in the context of Data Availability, and we should expect this to extend to our slightly different use-case of data dissemination.

Another factor in the cost of KZG is that it requires many operations over a group (in this case, an elliptic curve) which is at least an order of magnitude more expensive than a field operation. ZODA, on the other hand, performs only field operations, and inexpensive hashing. We should also expect the latency to be improved as well, requiring less time to compute the checking data for the shards.

Summary

A leader wants to send some data to followers.

In the naive case, the leader simply sends all of the data to everyone.

To optimize distribution, we encode the data into shards, with each follower receiving one shard. The data can be recovered from a subset of shards. The leader commits to the shards, so that we can easily check if purported shards actually belong. Unfortunately, we can’t know if the data is uniquely recoverable until re-assembling it, and re-encoding it to see if it matches our commitment.

ZODA alleviates this by guaranteeing that a shard originates from a valid encoding of the data, by adding additional checksums to each shard. Some more advanced schemes, like Ligerito can pave the way for verifying arbitrary properties of the sharded data, which we’re excited about.

Our initial implementation of this scheme can be found in the Commonware Library.

Looking to develop a better intuition for ZODA? Check out our podcast with Guillermo Angeris and Alex Evans from Bain Capital Crypto.